I am a computational physicist; more specific, condensed matter physics or materials science. I am proficient in high-performance computing, numerical optimization, and scalable computational skills to solve large-scale problems.

I received my physics PhD at the University of California, San Diego, and then spent a year to stay at the University of Illinois, Urbana-Champaign, as an electrical engineering postdoc fellow. After that, I stayed at the University of Texas at Austin for more than 3 years as a physics postdoc researcher before joining Insight. During my academic years, I developed several computational methods, incorporating with numerical techniques from physics and machine learning to solve large degrees of freedom problems.

I have published 30 papers with over 800 citations, and my Hirsch-index is 17 (at Google Scholar). I gave more than 20 invited talksover the world to share my research discovery. Here is a given lecture slides, from the 2014 ICAM-China summer school organized by Peking University, in Weihai, Shangdong, China.

Research Focus

My research focused on numerical simulations on exotic solid-state materials, such as topological insulators, superconductors, Weyl semimetal, unconventional superconductivity, in which physical properties (like electronic transport) are dominated by quantum mechanics; potentially, these systems are able to provide unprecedented applications (such as disspationless transport) in electronics and spintroics.

During my research projects, I have designed a variety of microscopic models to study material physics, and predicted possible exotic quantum phases which have not been seen experimentally. Usually, the state space of the microscopic models (in physics we called the Hilbert space) is huge. Supposed that there are q possible states on each lattice site, then for a N-site lattice, there are \( q^N \) degrees of freedom. On the other hand, at the atomic scale, the Coulomb's interaction between electrons makes the problem very complex. Even in the simplest model, such as the Hubbard model which considers the simplified interaction type, the complexity of the systems still grows up exponentially to prevent us against direct investigations.

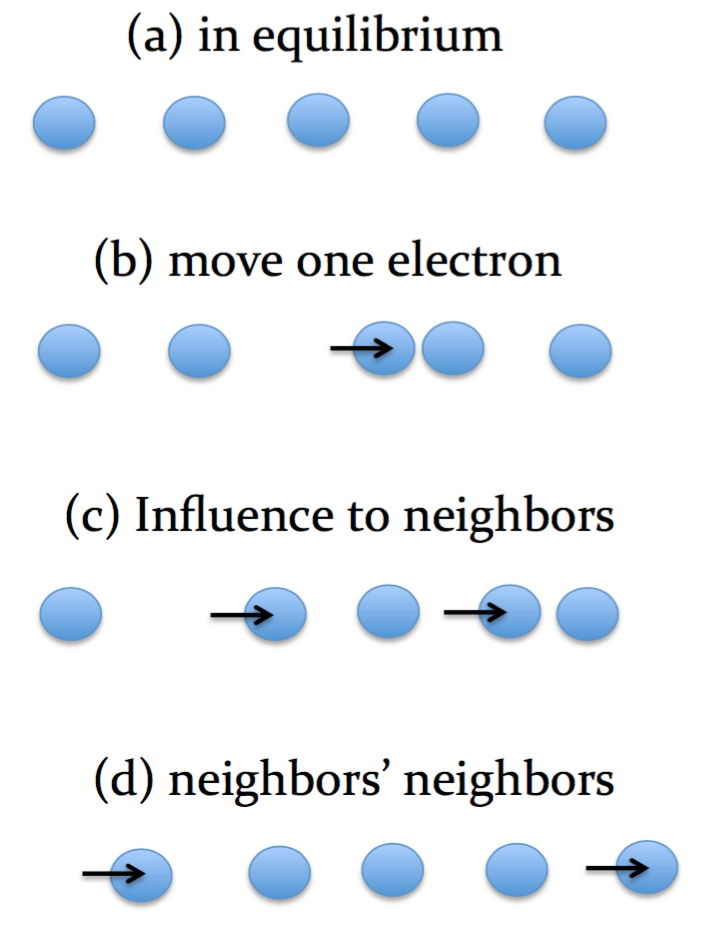
Supposed that a system is in equilibrium; each electron is staying at its equilibrium position, shown in the right figure (a). Now we move an electron away from the position, like (b). Such a change will result in raising the system's free energy, and being away from the equilibrium state. Then the electron's neighbors will respond to the change, move and search for their new equilibrium positions to lower the free energy [see (c)]. However, once the neighboring electrons move, the neighbors' neighbors need to do it either, and.... in (d). In such a manner, the physical response is globally rather than locally correlated, like a ripple; hence in the condensed matter community we call this system a correlated system.

I have designed a variety of high-performance computing techniques in distributed systems (meaning high-efficient parallel computation, up to thousand cores) to study the correlated materials. The methods includ Markov-chain Monte Carlo methods (MCMC), dynamical mean-field theory (DMFT), vortex BdG method, molecular dynamics, density matrix renormalization groups (DMRG) and Lanczos projection algorithm, a large-scale eigenvalue solver.

Connection to Machine Learning

Surprisingly, some of the numerical techniques, MCMC, DMFT and DMRG I have been familiar with, are in scenario similar to machine learning algorithms in data science. In physics, these numerical algorithms are essentially designed to reduce dimensionality of state space, which is proportional to complexity. In data science, MCMC can help us efficiently search for maximum likelihood of a graphic model, and has been proposed to learning a Bayesian network. Rather than directly solving complex models, DMFT implements conjugate gradient to build an effective predictive model, like linear regression. DMRG is an iterative numerical method to filter out important base states and truncates unnecessary complexity, which is analogous to principal component analysis for dimensionality reduction. In the algorithm page, I will explain the algorithms (try without using too much terminology) and connect to machine learning.